Speaker
Description
In a d-dimensional porous medium, d+1 Minkowski functionals are required to fully characterize the status of two-phase immiscible fluids (1, 2). If fewer variables are available, which is practically common, the hysteresis effect emerges that disables unbiased estimation of fluid properties. Therefore, researchers are making major efforts to reduce the number of functionals under certain circumstances (3, 4). Here, we show that, once bubbles (or droplets, ganglia) are mobilized, their hysteresis in porous media can be largely erased, which may significantly simplify the characterization of the multi-fluid dynamic porous medium.
We inherit a conceptual model describing bubbles residing in a homogeneous porous medium (5). An external field is imposed, whose intensity is evaluated by a modified Bond number $Bo_m$, defined as the ratio of the external field potential drop to capillary pressure, $P_{c}$. We track the bubble evolution under increasing $Bo_{m}$.
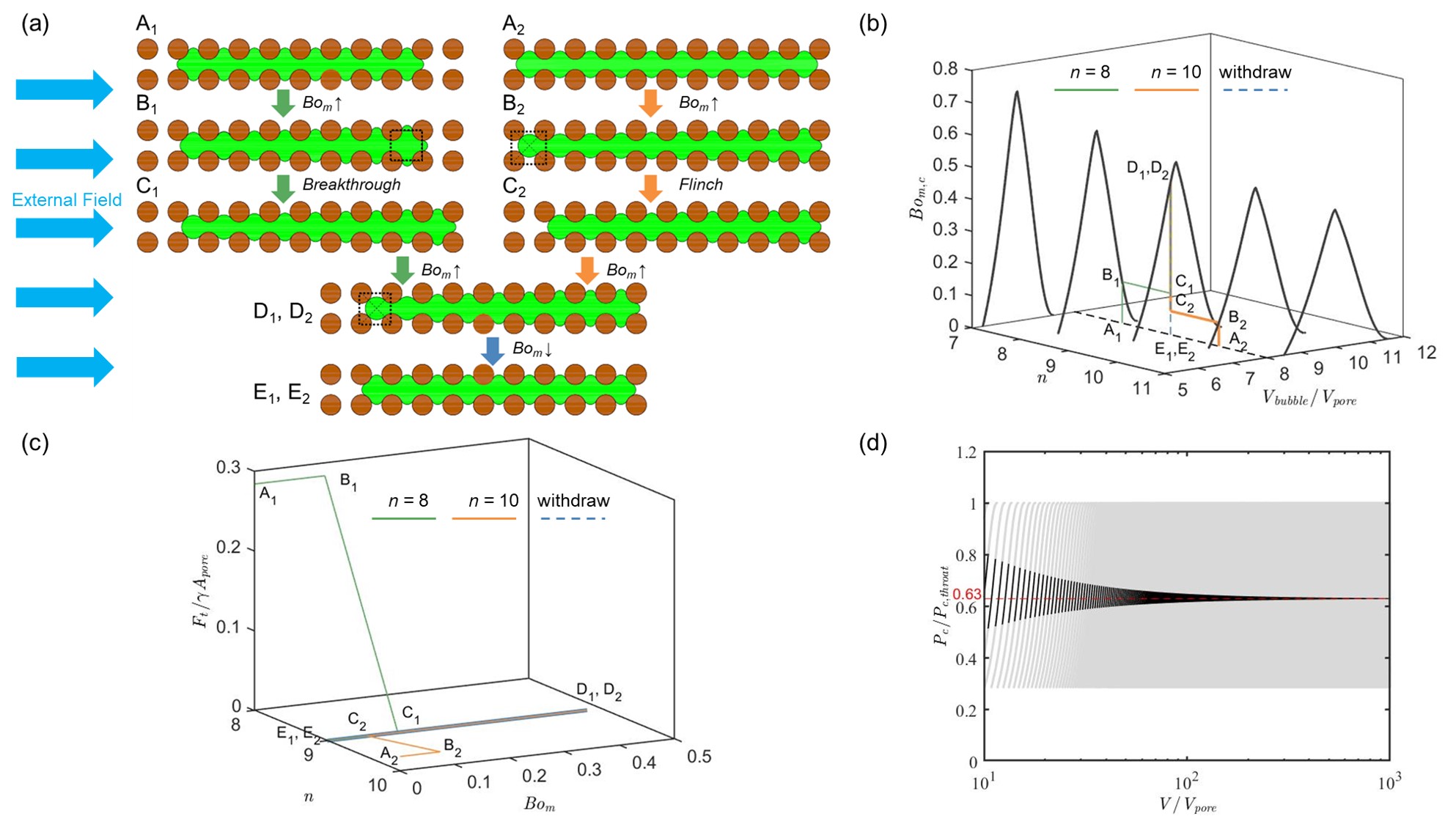
A surprising “normalization” effect is revealed before a bubble is finally mobilized: regardless of its multiple possible initial pore-occupancies, capillary pressures, and surface area (5), the bubble gradually evolves towards a specific morphology when $Bo_{m}$ keeps increasing. During the normalization, the bubble behaves as a wriggling worm that repeats two modes: (1) reversibly deforms to balance the external field without changing pore occupancy, and (2) irreversibly marches its head outwards or withdraws its tail inwards thus changing pore-occupancy by one. [Fig.1a] Finally, at the critical Bom,c, the bubble starts to flow, and it reaches a final state with a minimum total energy [Fig.1b&1c].
Furthermore, we find that $P_{c}$ of bubbles in their final states, regardless of their sizes, fall into a very narrow interval around a constant, $P_{c}^*$, although their initial $P_{c}$ vary in a much wider range. This final $P_{c}^*$ depends only on the pore-throat structure, regardless of bubble size and initial morphology [Fig.1d]. Similar evolution towards a constant also happens for the specific surface area or molar free energy. Thus, we can now give an unbiased and precise estimation on dispersed phase properties, without the need to know pore-scale details like Euler characteristics, pore occupancy, etc., if the bubbles experienced mobilization. In other words, mobilization erases bubbles’ hysteresis.
Despite limitations in heterogeneity and wettability, we believe our simple analysis successfully captures the essence of how bubbles are mobilized under external fields and how mobilization erases hysteresis. This discovery is aligned with previous simulations and experiments that we re-visit (6, 7), and could be applied to significantly simplify the modeling of two-phase immiscible flow in porous media.
References
- R. T. Armstrong et al., Porous Media Characterization Using Minkowski Functionals: Theories, Applications and Future Directions. Transport in Porous Media 130, 305-335 (2018).
- J. E. McClure et al., Geometric state function for two-fluid flow in porous media. Physical Review Fluids 3, 084306 (2018).
- J. E. McClure, T. Ramstad, Z. Li, R. T. Armstrong, S. Berg, Modeling Geometric State for Fluids in Porous Media: Evolution of the Euler Characteristic. Transport in Porous Media 133, 229-250 (2020).
- J. E. McClure, M. A. Berrill, W. G. Gray, C. T. Miller, Influence of phase connectivity on the relationship among capillary pressure, fluid saturation, and interfacial area in two-fluid-phase porous medium systems. Phys Rev E 94, 033102 (2016).
- C. Wang, Y. Mehmani, K. Xu, Capillary equilibrium of bubbles in porous media. Proceedings of the National Academy of Sciences 118, e2024069118 (2021).
- K. M. Ng, A. C. Payatakes, Stochastic Simulation of the Motion, Breakup and Stranding of Oil Ganglia in Water Wet Granular Porous-Media during Immiscible Displacement. Aiche Journal 26, 419-429 (1980).
- K. M. Ng, H. T. Davis, L. E. Scriven, Visualization of blob mechanics in flow through porous media. Chemical engineering science 33, 1009-1017 (1978).
| Participation | Online |
|---|---|
| Country | China |
| MDPI Energies Student Poster Award | No, do not submit my presenation for the student posters award. |
| Time Block Preference | Time Block A (09:00-12:00 CET) |
| Acceptance of the Terms & Conditions | Click here to agree |