InterPore2019 Valencia

6 May 2019, 11:00 → 10 May 2019, 13:00 Europe/Madrid

InterPore2019 Valencia will be held at the The Valencia Conference Centre

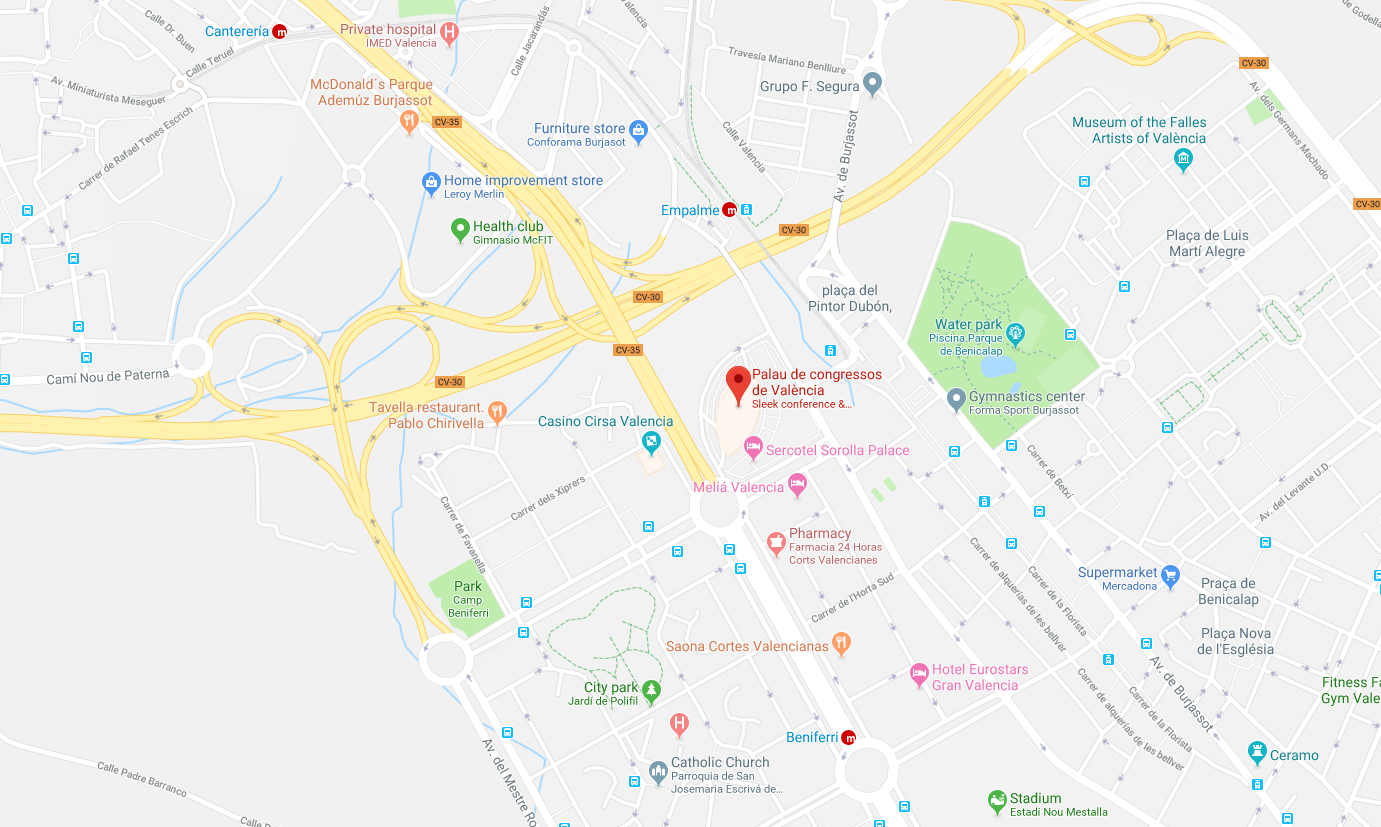
To get direct directions to the location click here

Interpore2019 is on Whova app! 

For more information visit our Whova page

Click on the image to watch a nice drone fly over the city hosting InterPore2019

Universitat Politècnica de València is organizing the Interpore 11th Annual Meeting from May 6th to 10th, 2019, in beautiful and sunny Valencia.

A city that bridges historical views

and modern landscapes The 11th Annual Meeting will be held at the Valencia Conference Center, a building that won the prize for World's Best Convention Center in 2010 and in 2018, surrounded by the conference hotels and only a short hop from downtown. Plan to attend, engage in cutting-edge research on porous media, and enjoy one of the most beautiful cities in Spain.

Conference technical program, important dates, accommodation details will be available shortly on the site.

The local organizing committee looks forward to welcoming you to Valencia in 2019.

---

Topics and applications

Transport phenomena Mathematical and computational modeling Interfacial behavior and multiphase flow Multiscale and multiphysics processes Experimental advances CO2 sequestration Imaging, microscopy, and micromodels Swelling porous media Reservoir simulation Groundwater hydrology Geomechanics and fractured materials Soil mechanics and engineering Pore-scale modeling and upscaling

Reactive flows Wave propagation Filters and membranes Fibers, wood, paper, and textiles Cements and construction materials Food and consumer products Biofilms, bone, & tissue Geothermal energy Biotechnology Composites and foams Fuel cells and batteries Novel porous media applications Nanoporous materials

---

Event Management
 

 

HotelFiles ACCOMMODATION_FORM.docx INTERPORE HOTELS 2019.pdf

Letters visa_letter_form.doc

Other Informations Detailed ProgramV4 Final.pdf Instructions for presenters and session chairs.docx

Short Course Speakers

• Andreas Yiotis.pdf
• Bernd Flemisch.pdf
• Edward Coltman.pdf
• Federico Gamba.pdf
• Ioannis Zarikos.pdf
• James McClure.pdf
• Katharina Heck.pdf
• Kilian Weishaupt.pdf
• Melanie Lipp.pdf
• Nikos Karadimitriou.pdf
• Sina Ackermann.pdf

Sponsor Informations

• EXHIBITORS REGISTRATION FORM.docx
• Information_for_sponsor_InterPore2018.pdf
• Information for Sponsors of InterPore2019.docx

Monday, 6 May

11:00 → 12:00 test

11:00 Pore-scale modeling of catalytic filters for automotive exhaust gas aftertreatment

Current automotive exhaust gas aftertreatment systems consist of catalytic converters for abatement of gaseous pollutants such as CO, hydrocarbons (HC) and nitrogen oxides (NOx), and a filter trapping the particulate matter (PM). So far only cars with Diesel engines have been equipped with the filter (DPF) but the recently introduced EURO 6c particulate number limits enforce the use of particulate filters also with gasoline engines (GPF). Both catalyst and filter have the shape of a cylindrical monolith with a large number of parallel channels in a honeycomb arrangement. However, standard catalytic converters are flow-through while the filter channels are alternately plugged at the inlet or outlet so that the exhaust gas is forced to permeate through the porous wall from one channel to another, filtering out the soot. To make the system more compact, the catalytic material can be deposited directly into the filter as on-wall layer or inside the porous wall. The advantages of catalytic filters are space, weight and cost savings, reduction of overall heat-losses and easier soot combustion in the presence of catalyst. On the other hand, the distribution of catalytic material on or in the porous filter walls has to be carefully optimized to meet the opposing requirements of maximum filtration efficiency, high conversion, and minimum pressure drop.

In this contribution we introduce a newly developed methodology for the pore-scale simulation of gas flow, diffusion, reaction and soot filtration in the coated catalytic filter. 3D morphology of the porous filter wall including the actual distribution of catalytic material is reconstructed from X-ray tomography (XRT) images and further validated with the mercury intrusion porosimetry (MIP). The reconstructed medium is then transformed into simulation mesh for OpenFOAM. Flow through free pores in the substrate as well as through the coated zones is simulated by porousSimpleFoam solver, while an in-house developed solver is used for component diffusion and catalytic reactions. Transport and filtration of soot particles is calculated with Lagrangian model including Brownian motion. Three filter samples with different distribution of alumina-based coating ranging from in-wall to on-wall are examined. Velocity, pressure and component concentration profiles are calculated enabling the prediction of permeability, component conversion and filtration efficiency depending on the actual microstructure of the wall. The simulation results suggest that the gas predominantly flows through remaining free pores in the filter wall and cracks in the coated layer. The mass transport into the coated domains inside the filter wall is enabled mainly by diffusion. Large domains of compact catalytic coating covering complete channel wall result in a significant increase of pressure drop as the local permeability of the coating is two orders of magnitude smaller than that of bare filter wall. The spatially averaged results of pore-scale model are then employed in the entire device model. The predictions are in good agreement with the measured pressure drop, conversion and filtration efficiency. From the studied samples, the most promising structure is the one combining in-wall and partial on-wall coating. The developed models provide useful feedback for further optimization.

Speaker: Prof. Petr Koci (University of Chemistry and Technology, Prague)

Monolith research group - web page

MS9_MP1_Monday_1415_Koci.pptx

11:15 Fluid displacement and trapping during two-phase steady-state flow in complex carbonate imaged by synchrotron x-ray microtomography

Multiphase fluid flow has been intensively studied within relatively homogeneous pore structures such as bead packs and sandstones. It has been shown that pore network characteristics such as the network topology, the pore size distribution and surface morphology can strongly affect the displacement and trapping of fluids by varying local capillary pressure and thereby changing the preferable path of fluids. In more complex media such as carbonates, fluid displacement and trapping in highly tortuous pore networks comprised of multiscale porosity are less-well understood. To find out how these factors impact the process, we conducted in-situ two phase core-flooding experiments in an oolitic Indiana Limestone with multiscale pore size and two different pore surface morphologies at the microtomography beam lime 2-BM at the Advanced Photon Source. The 3 mm diameter, 10 mm long core was saturated with oil, then flooded with brine to an irreducible oil saturation, followed by oil re-injection and steady-state (oil and water simultaneously) injection, using potassium iodide brine and dodecane as aqueous and oil phase, respectively. The entire injection process was imaged in 4D using 1-second 3D data acquisition in 20 second intervals. The excellent microtomographic data with a spatial resolution of 2.2 micron per pixel allowed visualisation of fluid flow in the sample and quantitative analysis of pore-scale fluid displacement processes. Here we show 4-dimensional data of 1) fluid trapping and displacement in a complex pore structure during drainage and imbibition. 2) The effect of two different surface morphologies, smooth, drusy calcite surfaces and rougher oolite surfaces, on the contact angle and fluid saturation. We found that in this specific pore structure, steady state injection of two fluids does not lead to a monotonic saturation change that occurs in non-steady-state injection or reaching a steady saturation level, but a sinusoid saturation - desaturation - resaturation behaviour in the recorded time-lapse. At this stage of our ongoing interpretation we believe that this is caused by a dynamic competition of two immiscible fluids that both have the access to the same complex pore space. The pore surface morphology may influence this competition by partially altering local contact angles within pores, therefore causing a complex local capillary pressure. This study provides insights on fluid behaviour in complex pore structures and varied pore surface topology during steady-state flow, which are beneficial for improving fluid simulation predictions.

Speaker: YILI YANG (University of Edinburgh)

MS6_A3A_Monday_1415_Yang.pptx

11:30 Flow and heat transfer in a microchannel partially filled with a microporous foam involving effects of flow inertia, flow/thermal slips, thermal non-equilibrium and thermal asymmetry

A theoretical study of forced convection in a parallel-plate microchannel partially filled with a porous medium is performed based on the local thermal non-equilibrium (LTNE) model. The two walls sandwiching the channel are exposed to thermal asymmetry boundary conditions, and the flexible porous medium is not connected to the walls. Effects of flow inertia in porous medium, velocity jump at the porous/fluid interface, and flow slip and thermal slip at the solid/fluid interface are involved. Exact solutions are obtained for velocity and temperature in both porous medium region and fluid region. The flow heterogeneity coefficient defined for describing the nonuniform distribution of fluid flow is especially considered, and the effect of flow heterogeneity on heat transfer is revealed. The entropy generation analysis is performed for heat transfer and fluid friction irreversibilities in the channel partially filled with a porous medium. The benchmark solution provided in this work can be used for improving numerical scheme accuracy and validating similar research.

Speaker: Prof. Huijin Xu (Shanghai Jiao Tong University)

Interpore-Huijin Xu.pptx

11:45 Impact of PTFE distribution on water transport in a gas diffusion layer of polymer electrolyte fuel cells

In polymer electrolyte fuel cells (PEFC) the transport of liquid water is highly relevant for efficient operation of the stack. For this reason the liquid water transport in gas diffusion layers (GDL) and in channels is addressed by many researchers. The GDL/channel interface is characterized by Yu et al. [1,2], its coupling to channel simulations is shown by Andersson et al. [3]. In that work the GDL fibers were assumed being hydrophobic by covering them with polytetrafluorethylene (PTFE) completely. On the other hand it is known that the PTFE distribution on the outer surfaces and inside the GDL is not homogeneous [4].

In this work the impact of PTFE distribution inside the GDL on transport properties will be discussed.

The water transport simulations in the GDLs are performed in micro structures created by a stochastic geometry model [5]. These geometries are transferred to the lattice Boltzmann (LB) simulations via a series of binary images. Since the local hydrophilic / hydrophobic properties of the micro structure have a strong impact on two-phase flow behaviour inside the GDL, a distribution of the hydrophobing agent PTFE on the fiber surface is taken into account. A certain range around random positions within the GDL can be hydrophobized until a total amount of the GDL surface is covered. This algorithm can be applied to the whole GDL or to particular sub-regions of it resulting in local different contact angles of water on the solid fibers.

The water transport in a hydrophobized GDL is simulated for several total amounts of PTFE. The studies are applied for homogeneous and also for inhomogeneous PTFE distribution. The amount of PTFE and its homogeneity of distribution can cause systematic impact on the liquid water transport. However; the distribution of a given total amount of PTFE lower than 100 % leads to statistical spread when several realizations of PTFE distribution are applied to a fixed geometry.

The impact of the pore-scale distribution of PTFE on macrospcopic flow behaviour is discussed.

Part of this work was funded by the Chinese Scholarship Council (CSC), grant 201408080011. Transport simulations are running on hardware of the Jülich Supercomputing Centre, grant JIEK30.

Speaker: Dieter Froning (Forschungszentrum Jülich GmbH, Germany)

MS16_R2_Wednesday_0938_Froning-v4-16_9.pptx

11:45 Impact of wind action and medium physical properties on horizontal pore gas flow in near-surface porous media.

Wind action at the soil surface potentially controls the movement of gases (including greenhouse gases and water vapor) in the near-surface soil as well as exchange of these gases with the atmosphere. Part of the mechanism behind this gas movement has recently been shown to be wind-induced horizontal pore gas movement within the near-surface soil.
The objective of this study was to investigate how these wind-induced horizontal pore gas velocities depend on near-surface wind speed, wind gustiness, soil gas permeability, and distance to the soil surface.
Velocity profiles for wind-induced, horizontal pore gas flow as a function of soil depth in the top 15 cm of the soil, were determined using a recently presented tracer tracking method for measuring wind-induced pore gas velocity profiles in porous media. Measurements were carried out using two dry, granular porous media for different combinations of wind speed, wind gust frequency and medium particle size, in a wind tunnel to assure controlled conditions. N2 was used as tracer gas. Media particle sizes were 1.18 – 2.36 mm and 4.75 – 10 mm, exposed to wind speeds of up to 6 ms-1 and gust frequencies up to 1 Hz. Experiments were based on the 2k factorial design.
Results indicate, that average wind speed, wind gustiness and soil medium physical properties, all have a significant influence on both absolute horizontal pore gas velocities, as well as on the overall shape of the pore gas velocity profiles as a function of soil depth.

Speaker: Dr Tjalfe Poulsen (Guangdong Technion Israel Institute of Technology)

MS8_A3B_Wednesday_1547_Poulsen.pptx

11:45 Insight into Influence of Crossflow in layered Sandstone porous media during Miscible and Immiscible CO2 WAG Flooding

For the layered system, cross-flow is one of the mechanisms for recovery enhancement during an IOR/EOR process. Thus, the results from this paper are very important to overcome the current challenges in capturing the importance of cross-flow influence as well as mitigating the effect of geological uncertainties on current and future IOR/EOR projects.
This manuscript presents the results of an experimental investigation into the effect of cross-flow on ultimate oil recovery during miscible and immiscible CO2 WAG flooding in layered sandstone porous media. A manufactured core sample constructed by attaching two half-cylindrical homogeneous natural sandstone plugs of different permeabilities. The core flooding tests using n-Decane Synthetic brine CO2 were conducted at a constant temperature of 343 K and under two different pressure conditions, namely, 9.6 MPa and 17.23 MPa to attain both immiscible and miscible conditions, respectively.
The results indicated that cross-flow in the layered sample has a negative impact on the ultimate oil recovery (i.e. decreasing oil recovery factor). The degree of heterogeneity seems to strongly influence the effectiveness of cross-flow during CO2 EOR with the oil recovery decreases as the permeability ratio (PR) between the two half plugs included in every samples increase. For instance, during miscible CO2 WAG flooding, a decrease in incremental oil recoveries from 3.3% to 11.3% and eventually to only 4.8% occurred when the permeability ratios were increased from 2.5 to 5 and 12.5, respectively. Similarly, during immiscible displacement, the recorded oil recoveries were 6.1%, 6.9% and 4.7% reflecting the same increases in permeability ratios as above. These results revealed that cross-flow works against the influence of the dominant active forces. For instance, in non-communicating layers, the dominance of viscous forces prevailed while there is a preferential flow path exists in flow in communicating layers. However, with increasing permeability ratio a considerable channelling of CO2 into the high permeability layer leaving the low permeability layer touched partially, implying that heterogeneity in vertical direction indeed significantly affects remaining oil saturations, thus oil recovery.

Speaker: Duraid Al-Bayati (Faculty of Science and Engineering, School of WASM-MECE, Curtin University)

MS8_A3B_Wednesday_1620_Arjomand.pptx

11:45 Taylor Dispersion: Evolution from the Initial Condition

After nearly 65 years of research on Taylor dispersion and literally thousands of papers on the subject, it is reasonable to ask if there is anything interesting left to be said about it. However, there still remains one outstanding problem in Taylor dispersion theory that has resisted a very satisfactory theoretical description. This is the problem of the relaxation of the initial condition at so-called “early" times in the Taylor dispersion process. Although a number of methods have been proposed, the constraints on the results are usually quite severe (e.g., asymptotic expansions that are only valid for exceptionally small times, or formulations that apply only to particularly simple configurations).

In this talk, we will discuss some of the history of this problem, and recent results that have been obtained by our group for describing the full range of the transport process from early to asymptotically-long times. Our approach is based in conventional PDE theory, and a somewhat unconventional approach to averaging. In particular, we derive an effective mass balance evolution equation not scale invariant upon averaging. The averaged equation contains an exponentially decaying (in time) source term that does not appear in the original microscale balance. The role of this source term is to account for the relaxation of the initial condition by redistributing mass within the domain (hence, the integral of the source term over the entire domain is zero). This leads to a final result that is able to represent spatially non-symmetric distributions of the average concentration at early times, and approaches the conventional Taylor-Aris result at asymptotic times. We compare the results of our upscaled representation with those computed from direct numerical simulation at the microscale; good fidelity between the two methods is observed. The approach has interesting applications to other kinds of systems where upscaling in the proximity to specific initial configurations (e.g., reactive transport; ecological dynamics) is important.

Speaker: Brian Wood (Oregon State University)

wood_main.pdf